325. Dangerous route

In a certain country, there are n cities, some of which are connected by two-way roads. The cities are numbered from 1 to n. During a financial crisis, crime rates soared, and organized criminal groups began to emerge. As a result, traveling along certain roads became dangerous.

Baha needs to travel from city 1 to city n. Since he values both his life and his possessions, he decides to outsmart the robbers by choosing the safest route, even if it’s not the shortest. For each road, he has assigned a danger level, represented by an integer between 0 (completely safe) and 10⁶ (extremely dangerous). The danger of a route is determined by the most dangerous road on that route.

Help him find the safest possible route (i.e., the route with the lowest maximum danger).

Input. The first line contains two integers n and m (2 ≤ n, m ≤ 10⁶). Each of the next m lines describes one road and contains three integers:

· a, b – the cities, connected by the road (1 ≤ a, b ≤ n);

· c – the danger of the road (0 ≤ c ≤ 10⁶).

Multiple roads may exist between any two cities.

Output. Print one integer – the danger of the safest route.

Sample input 1	Sample output 1
3 2 1 2 1 2 3 1	1

Sample input 2	Sample output 2
6 7 1 2 1 2 3 2 3 4 3 4 6 5 2 6 10 2 5 7 5 6 1	5

SOLUTION

data structures – disjoint set

Algorithm analysis

Sort the roads (edges of the graph) in ascending order of danger. To solve the problem, we’ll use a disjoint-set (union-find) data structure. Initially, we form n sets, each containing one vertex. Iterate over the edges in ascending order of danger. For each edge (a, b), merge the sets containing vertices a and b. Once vertices 1 and n belong to the same set, the algorithm terminates. At that point, a path from vertex 1 to vertex n will exist, and the danger of the roads on this path will not exceed the danger of the last edge considered.

Thus, if after processing edge (x, y), the representatives of vertices 1 and n coincide, the danger of the safest route will be equal to the danger of road (x, y).

Example

In the first test case, the danger of the safest route is 1.

Consider the second test case.

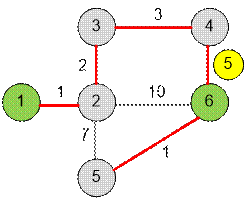
The edges are processed in ascending order of their danger. Once an edge with a danger of 5 is processed, vertices 1 and 6 will be connected, and the algorithm will terminate.

Algorithm implementation

Declare an array mas, used by the disjoint-set system. The edges of the graph will be stored in array e.

#define MAX 1000001

int mas[MAX];

struct Edge

{

int x, y, danger;

} e[MAX];

The Repr function finds the representative of the set containing vertex n. To avoid a Time Limit verdict, a heuristic is used: if the representative of vertex n is x, then mas[n] should be set to x.

int Repr(int n)

{

if (n == mas[n]) return n;

return mas[n] = Repr(mas[n]);

}

The Union function merges the sets containing vertices x and y.

int Union(int x,int y)

{

int x1 = Repr(x),y1 = Repr(y);

mas[x1] = y1;

return (x1 != y1);

}

Declare a comparator lt for comparing edges. The roads are sorted in ascending order of their danger.

int lt(Edge a, Edge b)

{

return (a.danger < b.danger);

}

The main part of the program. Read the number of cities n and roads m.

scanf("%d %d",&n,&m);

Initialize the array mas.

for(i = 1; i <= n; i++) mas[i] = i;

Read the edges of the graph into the array e.

for(i = 0; i < m; i++)

scanf("%d %d %d",&e[i].x,&e[i].y,&e[i].danger);

Sort the edges in ascending order of danger.

sort(e,e+m,lt);

Iterate through the edges, starting from the least dangerous one. Merge the sets containing their vertices. Once vertices 1 and n are in the same set (Repr(1) becomes equal to Repr(n)), the safest path will be found. Its danger will be equal to the danger of the last processed edge, that is, e[i].danger.

for(i = 0; i < m; i++)

{

Union(e[i].x,e[i].y);

if (Repr(1) == Repr(n)) break;

}

Print the answer.

printf("%d\n",e[i].danger);

Java implementation

import java.util.*;

class Edge

{

int x, y, danger;

Edge (int x, int y, int danger)

{

this.x = x;

this.y = y;

this.danger = danger;

}

};

public class Main

{

static int mas[], size[];

static int Repr(int n)

{

if (n == mas[n]) return n;

return mas[n] = Repr(mas[n]);

}

static boolean Union(int x,int y)

{

x = Repr(x); y = Repr(y);

if(x == y) return false;

if (size[x] < size[y])

{

int temp = x; x = y; y = temp;

}

mas[y] = x;

size[x] += size[y];

return true;

}

public static class MyFun implements Comparator<Edge>

{

public int compare(Edge a, Edge b)

{

return a.danger - b.danger;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

mas = new int[n+1];

size = new int[n+1];

for(int i = 1; i <= n; i++)

{

mas[i] = i;

size[i] = 1;

}

Vector<Edge> v = new Vector<Edge>();

for(int i = 0; i < m; i++)

{

int x = con.nextInt();

int y = con.nextInt();

int dust = con.nextInt();

v.add(new Edge(x,y,dist));

}

Collections.sort(v, new MyFun());

int index = 0;

for(int i = 0; i < m; i++)

{

Union(v.get(i).x,v.get(i).y);

if (Repr(1) == Repr(n))

{

index = i;

break;

}

System.out.println(v.get(index).danger);

con.close();

}

Python implementation

Declare the structure Edge for an edge.

class Edge:

def __init__(self, x, y, danger):

self.x = x

self.y = y

self.danger = danger

def Repr(n):

if n == mas[n]:

return n

mas[n] = Repr(mas[n])

return mas[n]

The Union function merges the sets containing vertices x and y.

def Union(x, y):

x1 = Repr(x)

y1 = Repr(y)

mas[x1] = y1

return x1 != y1

The main part of the program. Read the number of cities n and roads m.

n, m = map(int, input().split())

Initialize the list mas, used by the disjoint-set system.

mas = [i for i in range(n + 1)]

Read the edges of the graph into the list e.

e = []

for i in range(m):

x, y, danger = map(int, input().split())

e.append(Edge(x, y, danger))

Sort the edges in ascending order of danger.

e.sort(key=lambda x: x.danger)

for i in range(m):

Union(e[i].x, e[i].y)

if Repr(1) == Repr(n):

break

Print the answer.

print(e[i].danger)